Slides for previous talks may be viewed here:
Talk1 Talk 2 Talk 3 Talk 4 Talk 5
The sixth and final meeting of the class consisted of two parts. In the first hour we looked at how we view/understand the state of the world with the final hour devoted to a discussion of the effects of ageing on our perception & decision making, and a brief presentation on what we can do to help our brains stay healthy.
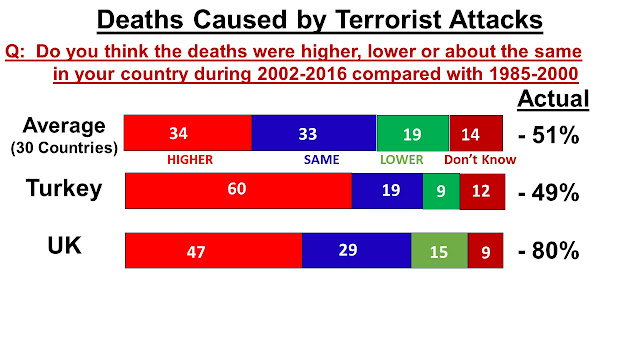
For the first part, I have relied heavily on the outcome and analysis of many IPSOS surveys which are nicely presented in Bobby Duffy's book 'The Perils of Perception'. In fact, in slide 1, I introduce the books that I have found useful in preparing the course material. Of course, there are many websites that provide excellent explanations on many aspects of the course covered in the six meeting.